geolinks: November 2017

Saturday, November 25, 2017

The 25 Interrelations of the Platonic Solids

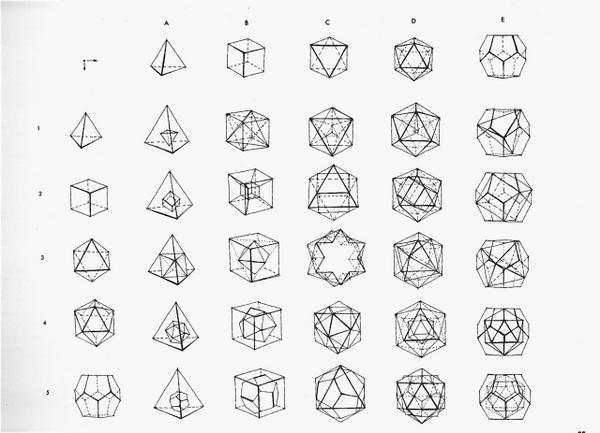
Once upon a time, back in the first years of the 1970s, I saw a page in Keith Critchlow's Order in Space that showed all 25 interrelations of the Platonic 5 Solids (tetrahedron, hexahedron or cube, octahedron, pentagonal dodecahedron, and icosahedron) and how they fit inside each other. Over the years, I built all 25.

I've also made magnetic models of some of these structures but not all of them and the nets are not all perfect but I did my best. A couple of times I've tried to send these nets to Critchlow but they were returned unopened. Oh well.

As with the Quanta Set that make up the Platonic Solids (http://geometrylinks.blogspot.com/2017/11/4-symmetrical-tetrahedra-of-5-platonic.html), I'd like see these built as class 2 tensegrities with spherical magnets at the vertices.

The following are the nets of the 28 different polyhedra that comprise the 25 Interrelations of the Platonic Solids.

Tetraset

HexaSet.1

HexaSet.2

Octaset

DodecaSet

IcosaSet.1

IcosaSet.2

Update: Originally, I transposed the tetra in dodeca net with the octa in dodeca net. The mistaken nets are below:

Thursday, November 16, 2017

4 Symmetrical Tetrahedra of 5 Platonic Solids

This is a video of a magnetic model of the Cube and the Tetrahedron broken down into its smallest symmetrical tetrahedra, what Buckminster Fuller called the A and B Quanta or mathematicians call Schläfli orthoschemes (I think).

The A and B Quanta make the equilateral triangle Tetrahedron (4 sided solid), square Cube or Hexahedron (6 sided), and equilateral triangle Octahedron (8 sided)

The A Quanta is 1/24th of a Tetrahedron, the smallest symmetrical tetrahedron to make up a Platonic solid. Here is the net of the A Quanta which can be folded to make the left and right hand versions, both of which are needed.

The B Quanta plus the A Quanta makes the Cube or Hexahedron
and the Octahedron,
two other Platonic solids
48 A Quanta + 24 B Quanta = 1 Cube
2 Cubes = 1 Octahedron

A third, the Dodeca Quanta, builds the Dodecahedron

120 Dodeca Quanta = 1 Dodecahedron

And a fourth,
120 Icosa Quanta = 1 Icosahedron

I've made magnetic models of the 5 Platonic solids with the magnets in the centers of the faces of the polyhedra. The A and B Quanta have the same volumes and I suspect share that volume at the same scale, all four tetrahedra share one common right angle triangle, but I haven't tested that hypothesis.

Since I saw this video, I think the next model should be a set of these Quanta built as class 2 tensegrities with ball magnets at the vertices. In fact, I'd commission someone to build it, for the right price.

Wednesday, November 1, 2017

Geometry Links - November 1, 2017

360º Book

https://youtu.be/jPea1Z1eQ6s

The Eyeballing Game

http://woodgears.ca/eyeball/index.html

Transforming paper sculptures (kami kara)

http://mymodernmet.com/karakuri-animal-puppets-haruki-nakamura/

http://kamikara.cart.fc2.com - shop

Visual math made with laser cutters

http://www.cherryarbordesign.com

http://www.cherryarbordesign.com/shop/

hat tip John Robb of Global Guerrillas

Don’t Fall for Babylonian Trigonometry Hype

https://blogs.scientificamerican.com/roots-of-unity/dont-fall-for-babylonian-trigonometry-hype/

Since I forwarded the hype, I now forward the rebuttal. Personally, I believe it’s turtles all the way down or, as the little old lady said, “If G*d had wanted us to fly, He wouldn’t have given us the railways.”

Fibonacci series animation

https://vimeo.com/9953368

3-D Printed Self-Folding Electronics

http://pubs.acs.org/doi/full/10.1021/acsami.7b10443

Victor Acevedo’s Instagram showing his geometric art

https://www.instagram.com/victoracevedo347/

Numericons - vector tiles for graphics, logos, patterns, and design, soon to be 10 sets of 100 tiles each

https://www.kickstarter.com/projects/markgonyea/numericons

http://markgonyea.net

Tensegrity

http://www.tensegriteit.nl

You can touch this tensegrity art